El otro día me encontré con un sencillo problema matemático. Un cuadrado dentro de un círculo. El cuadrado tiene 10 unidades por lado. La circunferencia del círculo toca todos los vértices del cuadrado y nos piden calcular un área sombreada.
Bueno una imagen dice más que mil palabras, este es el problema.
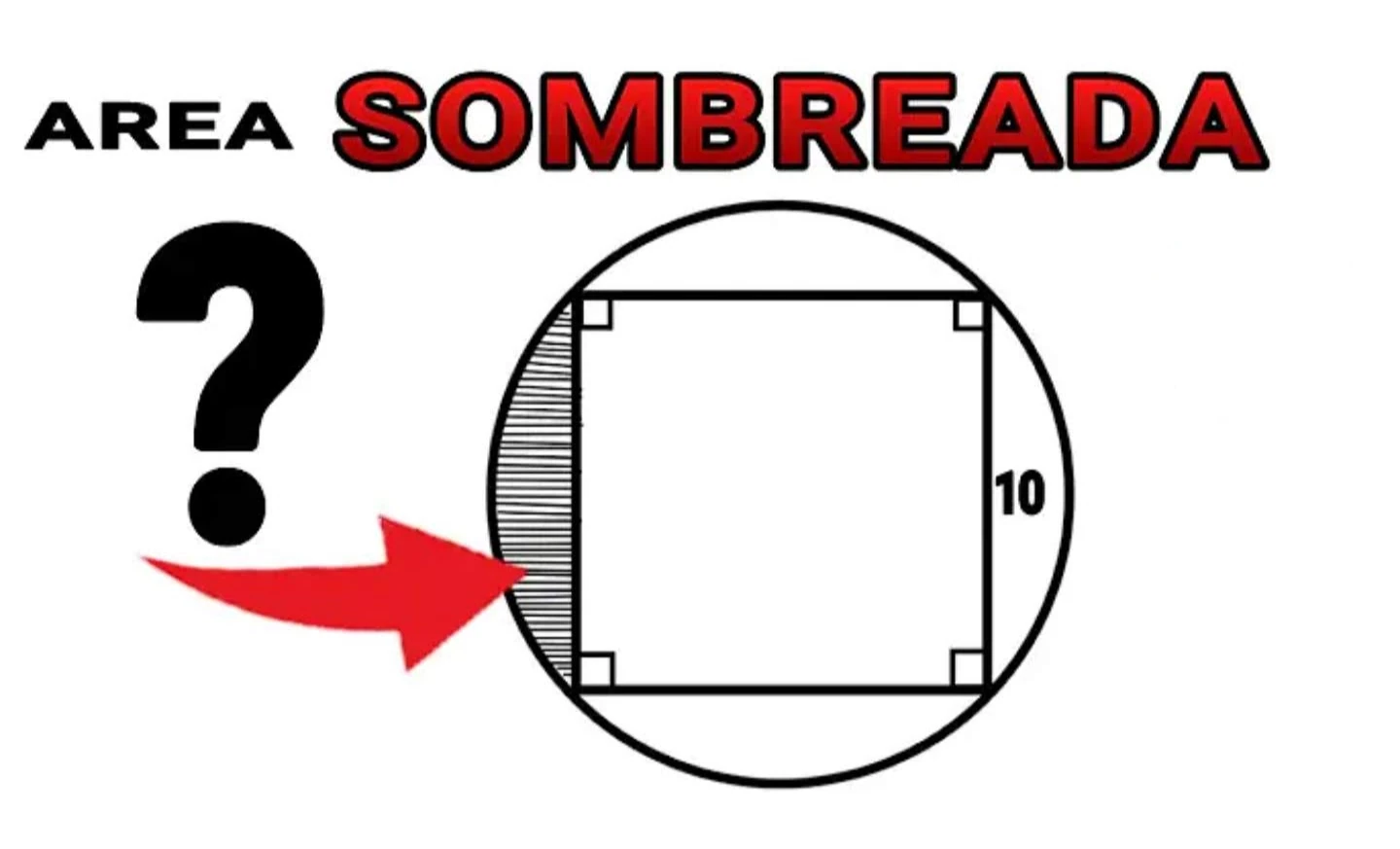
El planteamiento del problema. Calcular el área sombreada.
Me pareció interesante y se lo compartí a mis sobrinos y ahijados que están en edad escolar. Supongo que un alumno de primaria bastante avispado puede resolverlo.
Uno de secundaria, seguro debería de poder solucionarlo pero luego me di cuenta de varios problemas.
Entender el problema.
El primero fue entender el problema. Cuando vi la imagen para mi estaba claro, pero para otras personas no fue así.
Algunas personas necesitan que se les indique específicamente que es lo que deseas obtener. Calcular el área que está sombreada. Una persona fue demasiado lógica y dijo que el resultado era 10 ¿Se imaginan porque?
Pues porque si hay un 10 del lado derecho y las figuras son simétricas, entonces el área debe de ser la misma ¡Y no está mal su razonamiento!
Le tuve que explicar que el 10 es la longitud del lado del cuadrado (no el área).
En matemáticas buena parte del problema es el planteamiento del mismo. Pero hay un problema mucho más grave …
La apatía.

Definición de apatía por parte de la RAE.
Existe en nuestra juventud una tremenda apatía. Simplemente es más fácil no intentarlo, decir “no sé” que hacer un pequeño esfuerzo.
Y es que estamos compitiendo con un celular que es una fuente inagotable de distracciones, que en apariencia son más importantes que cualquier otra cosa en el mundo y eso mis estimados lectores, me preocupa.
¿Importan las matemáticas?
Entonces ¿Para que mandar los niños a la escuela? un colegio privado supone una mayor inversión y se supone que también una mejor calidad en la educación, pero nada de eso le gana a la apatía del alumno.
Ponemos el grito en el cielo por la falta de matemáticas en los libros de texto gratuitos , pero al mismo tiempo tenemos a una niñez pegada al celular perdiendo el tiempo.
Cuando uno se enfrenta a la materia de matemáticas muchas veces lo hacen con temor. Vamos, que tiene mala fama.
Hay frases que acompañan a la clase de matemáticas que todos conocemos o hemos escuchado como ¿Eso de que sirve?, o el “Lo vi en la escuela y nunca lo usé” y claro el “No le entiendo” todas son excusas de nuestro cerebro para evitar la fatiga.

Cuando dices ‘NO PUEDO’ tu cerebro se detiene. Cuando dices ‘¿CÓMO LO HAGO?’ tu cerebro comienza a trabajar.
Las matemáticas tienen un beneficio, expanden nuestra mente, nos abre a nuevas posibilidades de entendimiento y explican la razón de muchas cosas que nos rodean.
Un plomero que va a hacer un trabajo sabe que depende mucho de sus herramientas, si las tiene entonces su trabajo será más sencillo, hará un menor esfuerzo y terminará más pronto.
Si no las tiene entonces se tardará en terminar su labor, batallará mucho más y se cansará.
Las matemáticas son herramientas, es mejor tenerlas aunque no las usemos, que necesitarlas y no tenerlas.
Los niños son un caso especial, la edad ideal para aprender muchas cosas es durante la infancia. Su cerebro absorbe como esponja muchos conceptos. Después ya no les da tiempo.
Lamentablemente usan el celular como un medio de esparcimiento, todos mis sobrinos respondieron casi de inmediato a mi mensaje de whatsapp, pero ninguno logró resolver el problema. Bueno, uno lo intentó, pero no mucho, la verdad.
El celular es una herramienta fabulosa. Tienen tanta información a la mano y no la aprovechan, es un desperdicio de tecnología.
Okey, pero entonces ¿Cuál es el tamaño del área sombreada?
Para los que se quedaron a leer hasta este punto, no se preocupen, les comparto el resultado.
Básicamente hay que dividir el problema en varios más pequeños, muchos problemas se resuelven así.
- Calcular el área del cuadrado.
- Cálcular el área del círculo.
- Restar el área del cuadrado a el área del círculo y dividirlo entre 4.
El área del cuadrado es lo más fácil, un lado mide 10 entonces:
$ AreaCuadrado = 10 \times 10$
$ AreaCuadrado = 100$
El área del círculo tiene su truquito, aquí es donde nuestro buen amigo Pitágoras sale al rescate.
Es necesario calcular la hipotenusa para obtener el diámetro del círculo y con eso calcular el área.
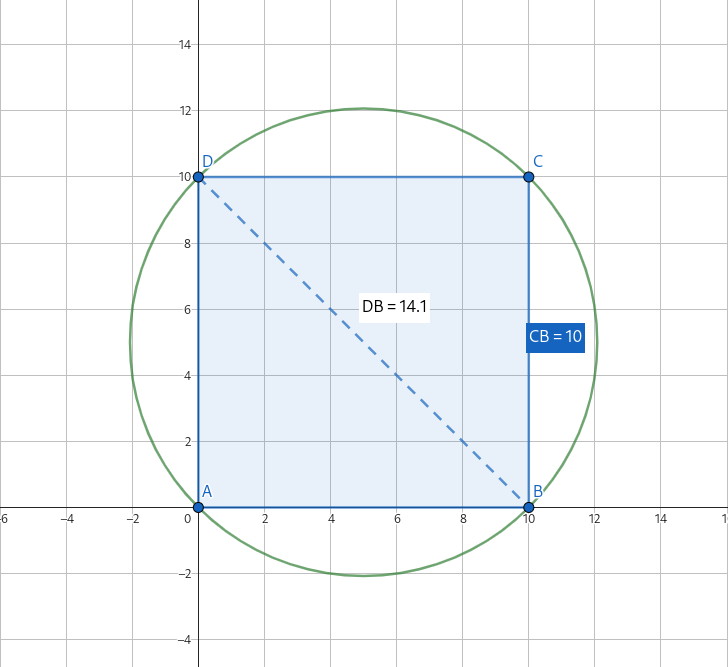
Clarificando el problema usando una gráfica de Geogebra.
Todos los lados del cuadrado miden lo mismo, así que calcular la hipotenusa es sencillo.
$ hipotenusa = \sqrt{10^2 + 10^2}$
$ hipotenusa = 14.14$
Para no complicar mucho las cosas, voy a usar la fórmula clásica para calcular el área de un círculo. Recuerden que la hipotenusa también es el diámetro del círculo.
Existe una fórmula para calcular el área de un círculo usando el diámetro, pero me pareció más sencillo dividir entre dos el diámetro para obtener el radio y de esa forma usar la fórmula que todos recordamos desde la primaria.
$A = \pi \times r^{2}$
$A = 3.1416 \times (\frac{14.14}{2})^{2}$
$A = 157.03$
Y con esta información tenemos todo para resolver el problema.
$AreaSombreada = \frac{157.03 - 100}{4}$
$AreaSombreada = 14.25$
Bueno 14.25 aproximadamente, todo depende del número de decimales que usas, pero si te acercas a esta cantidad el resultado es bueno.
¿Usted qué opina?
Me interesa saber la opinión de mis 4 lectores ¿Las matemáticas son importantes?, es necesario defenderlas para mejorar la educación de los niños o solo es una batalla perdida ante los grandes distractores como el celular y las redes sociales.
Si de por casualidad llegaste aquí buscando la solución al problema ¡Felicidades! al menos usaste el buscador, creo que a ninguno de mis sobrinos se les ocurrió ni eso.